De "Dimensie" van een Fractal
Bij het woord "Dimensie" denk je gewoonlijk aan de topologische dimensie. Dat is altijd een geheel getal: 0 voor een punt, 1 voor een lijn, 2 voor een vlak en 3 voor de ruimte.
Met de dimensie van fractals is wat 'raars' aan de hand.
Als je kijkt naar de Puntverzameling van Cantor dan zie je dat het geen losse punten zijn, maar lijnstukjes. Je zou
kunnen zeggen: "een verzameling van punten met een lengte".
Eenvoudig is in te zien dat de dimensie "ergens" tussen 0 en 1 moet liggen.
Iets dergelijks zie je bij (al of niet) vlakvullende kronkellijnen. Slechts een gedeelte van het vlak wordt gevuld
door een hoeveelheid lijnstukjes. Je zou ook kunnen zeggen: "een verzameling van lijnstukken met een breedte".
Eenvoudig is in te zien dat de dimensie "ergens" tussen 1 en 2 moet liggen.
Iets dergelijks zie je bij ruimtelijke fractals zoals de Spons van Menger. De dimensie zal daar "ergens" tussen 2 en 3 moeten liggen.
De conclusie moet luiden dat:
De dimensie van een fractal is een gebroken getal.
In 1977 introduceerde Mandelbrot de 'Fractal Dimension'. Hij noemde daarbij ook een formule, die een vereenvoudigde
versie is van de definitie van Hausdorff uit 1919.
De definitie van Mandelbrot stemt geheel overeen met de definitie van de 'capaciteit' van een meetkundige figuur (Kolmogorov, 1958).
Kolmogorov stelde voor om de lengte (van bijvoorbeeld de Puntverzameling van Cantor of een kustlijn) te meten in steeds
kleiner wordende stukjes h. Het kleinste aantal stukje om de verzameling op te meten noemen we N(h).
N is dus een functie van h. Als je h kleiner maakt wordt N groter. De dimensie D wordt
nu gedefinieerd als:
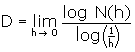
De term 'dimensie' heeft in de wetenschappelijke literatuur meerdere betekenissen. Wiskundigen gebruiken er al minstens vier. Het is daarom voor de duidelijkheid beter om van de capaciteit te spreken in plaats van de dimensie. De capaciteit van een punt, lijn, vlak en de ruimte is overigens gelijk aan de dimensie.
Deze website hanteert de aanduiding 'dimensie'; de term 'capaciteit' wordt verder niet gebruikt.
In onderstaande tabel wordt een overzicht gegeven van berekende dimensies van een paar fractals die op deze site zijn genoemd.
| Naam van de Fractal | D (benaderd) |
|---|---|
| Puntverzameling van Cantor | 0,6309 |
| Zeef van Sierpinski | 1,5849625 |
| Sierpinski tapijt | 1,892789260 |
| Kromme van Lévy | 1.934007183 |
| Gosper eiland | 1.12915 |
| Spons van Menger | 2,72683302028 |
| Kromme van Koch | 1,26186 |
| Worst van Minkowski | 1,5 |
| Logarithmische Spiraal | 1 |
© 2013-2025 webmasterij.nl | Disclaimer
| Contact | Privacy
Laatst bijgewerkt: 5 december 2013