Julia Fractals II:
Zuiver Imaginaire waarden van de constante
In het vorige hoofdstuk van deze verhandeling is gekeken naar het iteratie-proces:
zn+1 = zn² + c,
waabij c een reëel getal is. De oplossingen liggen allemaal in het complexe vlak, omdat z complex is.
Op deze bladzijde gaan we onderzoeken wat er gebeurt als c complex is, dus als c = x + iy.
Eerst bekijken we het gedrag van de Julia fractal bij de zuiver imaginaire waarden van c, dus c = iy.
Opmerking:
Een verhandeling over complexe getallen vind je HIER.
Zuiver imaginaire waarden van c
Het geval c = 0i is niet interessant; het is gelijk aan c = 0. Dat is in het voorgaande
al behandeld. De figuur is een cirkel met straal 1 waarbinnen alles wordt aangetrokken naar nul. Daar buiten treedt
divergentie op.
Als je c in stapjes groter maakt (nog steeds zuiver imaginair) zie je dat de oorspronkelijk cirkelvorm langzaamaan
verstoord wordt en ontaardt in iets dat lijkt op koraal. De figuren zijn niet spiegel-symmetrisch (zoals bij de reële
waarden van c) maar puntsymmetrisch ten opzichte van de oorsprong.
Hieronder staan de figuren die ontstaan bij verschillende waarden van c.

c = 0,1i

c = 0,5i

c = 0,7i
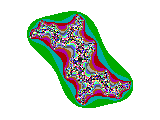
c = 0,8i
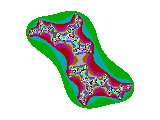
c = 0,9i
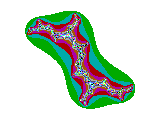
c = 1,0i
De gebiedjes waar nog aantrekking optreedt worden steeds kleiner en lijken bij c = 0,9i helemaal te zijn verdwenen. Dat is inderdaad zo. Voor c < -0,8i en c > 0,8i zijn er geen aantrekkers meer. In de figuur blijkt dat door het verdwijnen van het (hier zwart gekleurde) binnengebied. De grillige patronen blijven bestaan, maar worden al gauw oninteressant.
In de figuren neemt het aantal kleuren af. Dat betekent dat de divergentie erg snel gaat; functiewaarden van zn+1 = zn² + c gaan in een paar stappen naar oneindig.
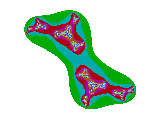
c = 1,1i
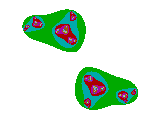
c = 1,3i

c = 2,0i
Hierboven is steeds een positieve factor bij i genomen. Als je een negatieve factor neemt ontstaat dezelfde figuur, maar gespiegeld in de imaginaire as.

c = -0,7i
c = +0,7i
 Opmerking:
Opmerking:
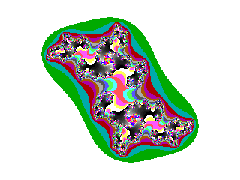
De plaatjes worden pas interessant als je er op in zoomt en als je een kleurenpalet met véél kleuren (-nuances) gebruikt.
Zie de figuur hiernaast, dat een detail is van de figuur voor c = +0.7i.
Het middelpunt van de figuur ligt op z = 0,2 - 0.48878i, vergroting 16×.
De figuren worden echter pas écht interessant als de constante c zowel een reëel deel als een imaginair deel heeft, zie het volgende hoofdstuk.
© 2013-2025 webmasterij.nl | Disclaimer
| Contact | Privacy
Laatst bijgewerkt: 12 december 2013