"Vreemde" Aantrekkers I:

Gewone enkelvoudige aantrekkers

Iteratieprocessen
Fractals kenmerken zich door oneindige herhaling. Als je fractals wiskundig wilt beschijven, kom je -dus- uit op steeds weer herhaald uitrekenen van dezelfde formule. Dat heet een iteratieproces.
Bij een iteratieproces vergelijk elke keer dat een formule is uitgerekend de uitkomst met de vorige. Na een (beperkt) aantal stappen stop je de herhaling. Dat kan zijn omdat je een bepaald aantal stappen hebt uitgevoerd, omdat het verschil in uitkomst tussen twee opeenvolgende stappen heel klein is geworden of omdat het resulaat van een berekening groter is dan een drempelwaarde.

Een voorbeeld van een iteratieproces is herhaald kwadrateren. Je kunt bijvoorbeeld 2² uitrekenen op een rekenmachine. Toets een 2 in en druk op x². Het resultaat is 4. Als je weer op x² drukt, krijg je 16, enz.
Op deze manier ontstaat de reeks: 2; 4; 16; 256; ..... enz. De getallen worden steeds groter. Op een gegeven moment houdt je rekenmachine er mee op. Het getal past niet meer in de rekenmachine.
Een iteratieproces waarbij de uitkomsten van de berekeningen steeds verder uit elkaar liggen, heet divergerend.

Er zijn ook convergerende iteratiepocessen. Dat heb je bijvoorbeeld als je herhaald gaat kwadrateren, maar begint bij 0,5.
Je krijgt dat de reeks: 0,5; 0,25; 0,0625; 0,00390625; .... enz.
De uitkomsten komen steeds dichter bij nul te liggen, maar worden nooit nul! De rekenmachine zal op een gegeven moment wel gewoon een nul laten zien, omdat het geen getallen kan weergeven die te dicht bij nul liggen.

Aantrekker
Herhaald kwadrateren van een getal x, -1 < x < 1 heeft altijd tot gevolg dat de uitkomst naar nul gaat. x = 0 wordt AANTREKKER genoemd.

Grafische weergave
Bij dit iteratie proces begin je met een getal, dat wordt gekwadrateerd. Het kwadraat wordt vervolgens gebruikt als invoer voor de volgende stap. Je hebt dus te maken met de grafieken van twee functies, namelijk y = x² (de parabool) en y = x (een rechte lijn). De grafieken zie je hier onder. Links staat het divergerende iteratie proces, rechts het convergerende. Het iteratiepoces is aangegeven met de groene lijn.
N.B.: We kijken alleen naar het snijpunt in x = 0.

 

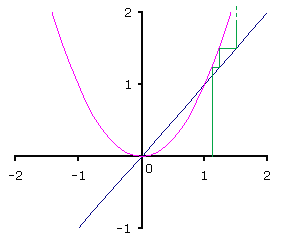
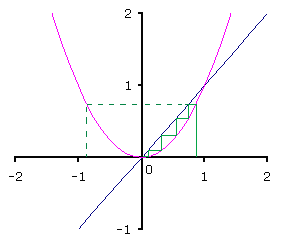
In de linker figuur begin je bij 1,1. Ga verticaal naar boven tot aan de parabool. Die bereik je bij 1,1² = 1,21. Ga vervolgens horizontaal naar de rechte lijn: x = 1,21. Ga vervolgens weer verticaal naar de parabool. Die bereik je bij 1,21² = 1,4641. Ga vervolgens weer horizontaal naar de rechte lijn: x = 1,4641. Vervolgens weer verticaal naar de parabool, enz. De kwadraten worden steeds groter: divergentie.

In de rechter figuur begin je bij 0,9. Ga verticaal naar boven tot aan de parabool. Die bereik je bij 0,9² = 0.81. Ga vervolgens horizontaal naar de rechte lijn: x = 0,81. Ga vervolgens weer verticaal naar de parabool. Die bereik je bij 0,81² = 0,6561. Ga vervolgens weer horizontaal naar de rechte lijn: x = 0,6561. Vervolgens weer verticaal naar de parabool, enz. De kwadraten komen steeds dichter bij nul: convergentie.

Eenvoudig is in te zien dat er ook divergentie gaat optreden als je begint met x < -1. Als je begint met -1 < x < 0 convergeert het proces ook.

N.B.: De strikt wiskundige formule voor dit iteratieproces luidt: x_n+1 = x_n²
Er is een reeks met x-waarden. De waarde van nummer n+1 in de rij is gelijk aan het kwadraat van nummer n in de rij (de voorgaande dus).
Dit is een oneindig doorlopende reeks. Je stopt echter met het uitrekenen van nieuwe waarden als het verschil (zonder het teken!) tussen twee opeenvolgende waarden kleiner is geworden dan een bepaald (klein) getal. In formule |x_n+1 - x_n| < t, t is bijvoorbeeld 10^-6 of nog kleiner.
Dit wordt het stopcriterium genoemd. In de grafiek is dat de lengte van horizontale groene lijn in het iteratieproces.

Een bijzonder geval : |x| = 1
Als x = 1 zit je in het snijpunt van de grafieken y = x² en y = x. De eerste stap voldoet dus gelijk aan het stopcriterium. De startwaarde x = 1 convergeert dus onmiddellijk naar het snijpunt in het punt (x,y) = (1,1).
Als je begint met x = -1 duurt het precies één stap langer...

Laatst bijgewerkt: 5 december 2013