"Vreemde" Aantrekkers II:

Gewone meervoudige aantrekkers

Een iets andere opzet
In het vorige hoofdstuk van deze verhandeling hebben we gekeken naar de grafieken van de functies y = x² (een parabool) en y = x (een rechte lijn). Het is interessant om eens te onderzoeken wat er gebeurt als je de parabool verticaal verschuift. De formule voor de parabool wordt dan: y = x² + c.
De formule voor het iteratieproces wordt nu: x_n+1 = x_n² + c.

De keuze van c
Convergentie treedt op als je in het 'gebied' kunt komen dat wordt omsloten door de grafieken van y = x² + c en y = x. Eenvoudig is in te zien dat het gebiedje kleiner wordt voor c > 0, en zelfs helemaal verdwijnt als c te groot wordt. De grafieken hebben dan geen snijpunt meer.

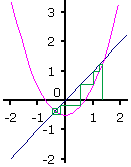
Als c < 0 wordt het gebied waar convergentie optreedt groter. Hiernaast staat de situatie getekend voor c = -0,5. Het iteratieproces is nu: x_n+1 = x_n² - 0,5.
Als je deze vergelijking analytisch oplost vind je snijpunten voor x = -0,366 en x = 1,366. Uit de figuur blijkt dat x = -0,366 de aantrekker is van alle startwaarden tussen x = -1,366 en 1,366. Er is echter nog steeds sprake van een enkelvoudige aantrekker.
Merk op dat de iteraties resultaten van het iteratieproces als een spiraal rond het snijpunt gaan draaien.

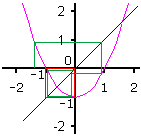Als je c = -1 neemt, gebeurt er iets merk­waardigs. Het iteratie­proces is nu: x_n+1 = x_n² - 1. De snij­punten zijn er voor x = -0,618 en x = 1,618.
Als je x = -1 invult, is het resultaat 0, maar als je x = 0 invult, is het resultaat -1. Het iteratie-poces gaat in een kringetje lopen en het snijpunt wordt niet gevonden. Dit wordt geïllustreerd in de figuur links met de rode lijn. De waarden x = 0 en x = -1 trekken elkaar aan! Dit wordt DUBBELE AANTREKKER genoemd.
Merk op dat het aantrekgedrag ook optreedt als je heel dicht bij het snijpunt begint; de resultaten verwijderen zich van het snijpunt en worden naar 0 en -1 getrokken.

Als je andere waarden van c kiest treden dit soort verschijnselen ook op, maar dan als vierdubbele, achtdubbele, enz. aantrekkers. Het steeds verdubbelen van het aantal aantrekkers heeft een naam: PERIODE VERDUBBELING.
Driedubbele aantrekkers komen ook voor.

Vreemde aantrekkers en chaos
Het verschijnsel van Periodeverdubbeling gaat niet tot in het oneindige door. Bij waarden van c kleiner dan ongeveer -1,4 gaat het systeem zich vreemd gedragen. Er zijn gebieden met startwaarden die worden aangetrokken, maar er is geen aantrekker aan te wijzen waar het iteratie proces naar toe leidt. De regelmaat is verdwenen.
Dit fenomeen wordt aangeduid met de term VREEMDE AANTREKKER.
Pikant detail: Soms komt de regelmaat hier -even- terug; in het chaos-gebied zijn gebiedjes te vinden waarin zich Gewone Aantrekkers bevinden.

Het iteratie-gedrag dat hier is beschreven wordt door wiskundigen aangeduid met chaotisch gedrag. De tak van de wiskunde die zich hiermee bezighoudt heet Chaos-theorie. Zie ook het volgende hoofdstuk.

Laatst bijgewerkt: 5 december 2013