Burning Ship Fractals

In het voorgaande is gekeken naar fractals van het type: z_n+1 = z_n^p + c. Hierin is z een complex getal en c is een reëel getal complex getal. In complexe notatie:
z = x + i y en c = a + i b. Voor b ≠ 0 is de figuur spiegel-symmetrisch, voor b = 0 is de figuur punt-symmetrisch.

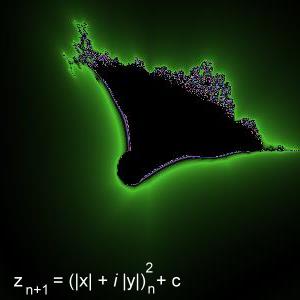
Behalve het variëren van p, kun je ook iets doen met x en y. Zo hebben Michael Michelitsch en Otto Rossler als eerste de formule gebruikt waarbij x en y zijn vervangen door hun absolute waarde. De formule wordt dan: z_n+1 = (|x| + i |y|)_n^p + c.

Bij nadere beschouwing van deze formule zou je denken dat er -net als bij de Mandelbrot-fractals- een symmetrische figuur ontstaat. Voor hogere waarden van p is dat inderdaad het geval, maar voor lagere waarden van p is dat niet meteen duidelijk. Voor p = 2 en c = (0,0) ontstaat de figuur hieronder.

Bij een geschikt kleurenpalet lijkt de figuur op een schip dat in brand staat. Daar komt ook de naam vandaan: "Burning Ship".
Dit is een fractal, want er is oneindige herhaling. Onderstaande figuur toont een detail van het schip, net voorbij de "achtersteven".

Hiervoor is al aangegeven dat de figuur ook voor hogere waarden van p kan worden gemaakt. Hieronder staan er een paar, voor p = 2 t.m. 7. De symmetrie is direct zichtbaar als p oneven is. Er is slechts één symmetrie-as. Bij even waarden van p zie je wel symmetrie ontstaan, maar voor "echte" symmetrie moet p veel hoger zijn dan hier wordt getoond.

Bron: theory.org/fracdyn/burningship/

Laatst bijgewerkt: 7 december 2020