Dendrieten
Op de beginpagina van deze verhandeling over de Wiskunde van Fractals is iets gezegd over de binaire boom. Als je het axioma anders kiest dan op de beginpagina, krijg je heel andere boomstructuren te zien. Je bent ook niet gebonden aan lijnstukken als basis. Je kunt ook uitgaan van eenvoudige meetkundige figuren zoals rechthoeken en driehoeken.
Twee-tallige Boom
Probeer eens het volgende voorschrift:
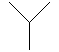
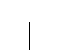 +
+
 =
=
Dit leidt tot een prachige boom, die is afgeleid van de Boom van Pythagoras, waarover later meer.
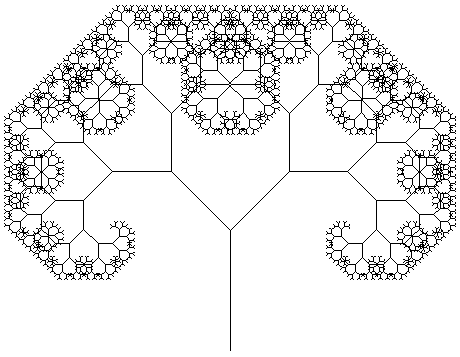
Deze boom is heel regelmatig. De natuur is niet regelmatig, dus er moet wat worden gedaan om een wat minder regelmatige structuur te krijgen. Dat bereik je door een zekere, beperkte, willekeurigheid aan te brengen in:
- De hoek waaronder de tak uit de stam ontstaat
- De orde tot welke een vertakking wordt doorgezet.
Op deze manier begint het er al aardig op te lijken, zeker als je aan het eind van elke vertakking nog wat "blaadjes" tekent. Zie onderstaande figuren.
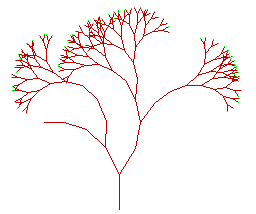

Opmerking: De soort wiskundige bewerkingen waar deze figuren uit voortkomen worden meestal aangeduid met de term IFS, dat staat voor Iterated Function System.
Realistische boom
 Het is niet erg realistisch om uit te gaan van een lijntje als basis als je een boom wilt genereren. Zowel basis als
motief hebben een dikte (dus 3-Dimensionaal!). Gebruik bijvoorbeeld zoiets als nevenstaande figuur als basis en
motief. Gebruik ook het patroon ("textuur") dat er op getekend is, maar varieer dat per stap.
Het is niet erg realistisch om uit te gaan van een lijntje als basis als je een boom wilt genereren. Zowel basis als
motief hebben een dikte (dus 3-Dimensionaal!). Gebruik bijvoorbeeld zoiets als nevenstaande figuur als basis en
motief. Gebruik ook het patroon ("textuur") dat er op getekend is, maar varieer dat per stap.
Om de stam dunner en korter te maken gebruik je verschillende factoren. Varieer daarbij tevens het aantal (1,2 of 3)
en de hoek tussen de takken onderling.
Varieer ook de orde per tak.
Op deze manier kun je een resultaat bereiken dat er bedrieglijk echt uitziet, in elk geval goed genoeg voor gebruik
in een computerspel of virtual reality omgeving.



Met behulp van kleur kun je nog mooiere effecten krijgen.
De strikte zelfgelijkvormigheid wordt hier bewust losgelaten, zij het gedeeltelijk. Zelfgelijkvormigheid volgt
uit de herhaling, niet andersom! De herhaling bepaalt immers of iets een fractal is...
Een mooie, tweedimensionale, uitwerking van deze benadering van een realistisch boom is te vinden op https://studio.yeahright.org/_projects/tree-the-sequel.
De Griekse Wiskundige Pythagoras (569 - 500 v. Chr.) heeft aangetoond dat voor een rechthoekige driehoek geldt dat:
a² + b² = c²
Hij deed door aan de rechthoekszijden a en b vierkanten te construeren en vervolgens aan te tonen dat de som van de oppervlakten van deze vierkanten gelijk is aan de oppervlakte van een dergelijk vierkant langs de schuine zijde c.
Door de redenatie om te keren kan dit gebruikt worden voor het maken van een mooie fractal-boom. Het vierkant met zijde c dient hierbij als basis. De driehoek en de beide andere vierkanten dienen als motief.
Driehoek met hoeken 45°, 45° en 90°:
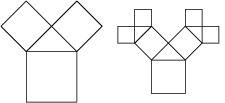
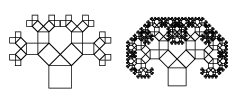
Opmerking: Als je de vierkanten vervangt door lijnstukken ontstaat de tweetallige boom aan het begin van deze bladzijde.
Driehoek met hoeken 30°, 60° en 90° (Scheve boom van Pythagoras):
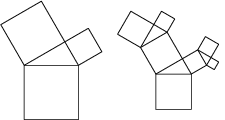
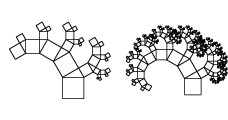
Opmerking: De takken in de boom van Pythagoras zijn spiraal-structuren die zich oneindig herhalen. Dat is
heel goed te zien bij de Scheve Boom. Ze worden logarithmische spiralen genoemd. In de levende natuur komen die
vaker voor o.a. in de schelp van slakken. De (fossiele) Nautilus-schelp is er een bekend voorbeeld van.
De Logarithmische Spiraal wordt verder besproken in het hoofdstuk 'Spiralen'.
Tot nu is er steeds gekeken naar varianten van de tweetallige boom. Maar er is geen enkele reden om je daartoe te beperken. Je kunt bijvoorbeeld ook een drietallige boom bedenken. Neem bijvoorbeeld een punt als basis. Vertrek uit dat punt met een rechte lijn onder een hoeken van 0°, +120° en -120° (0° is verticaal genomen). De schaalfactor per stap moet kleiner zijn dan 1. Hier is ½ genomen.
Zie onderstaande figuur. De boom is getekend tot orde 6. Uiteindelijk blijkt dit een stoffractal te zijn want de lengte van de lijnstukjes wordt steeds kleiner (maar wordt nooit nul).
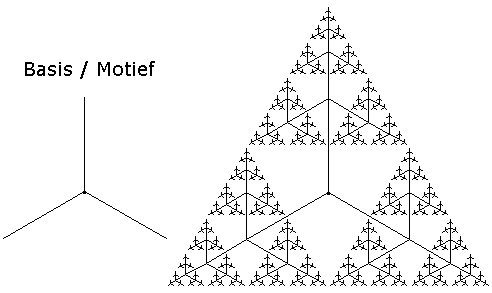
De driehoek die ontstaat als je de voorgaande stappen weglaat, staat bekend onder de naam Zeef van Sierpinski, naar de Poolse wiskundige Waclaw Sierpinski (1882 - 1969).
Deze fractal kan ook op een andere manier worden getekend. Ga uit van een gelijkzijdige driehoek (basis) en verwijder daaruit de driehoek zoals aangegeven. Als je dit herhaalt ontstaat weer de Zeef van Sierpinski.

Opmerking: Doordat de driehoekjes steeds kleiner worden, wordt ook dit weer een stof-fractal. Beide uitvoeringen van deze fractal leiden tot hetzelfde resultaat.
Opmerking: Deze laatste methode werkt precies andersom als bij het maken van de boomstructuren. Wordt er bij de boomstructuren steeds iets toegevoegd, bij de laatste methode wordt er steeds iets weggenomen.
Opmerking: Het is bij deze twee methodes niet nodig om uit te gaan van gelijkzijdige driehoeken. Elke willekeurige driehoek leidt tot een "Zeef". Je kunt deze fractal ook maken met rechthoeken. De naam die daaraan is gegeven is "Sierpinski-tapijt".

Opmerking: Dit soort figuren bedekt -in de limiet naar oneindig- een deel van het platte vlak. Ze kunnen daarom ook als "Vlakvulling" worden gezien. Vlakvullingen worden besproken in het volgende hoofdstuk.
Andere, bekende Iterated Function Systems

Varen van Barnsley

Draak

Koraal

Kristal

Spiraal

Gedwarrel
Andere Iterated Function Systems: Sterfractals
Behalve met lijnen en punten kun je ook fractals construeren met een veelhoek als uitgangspunt. De figuren die dan onstaan worden "Sterfractal" genoemd. Een paar voorbeelden:
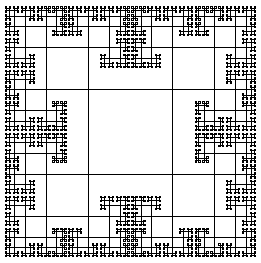
Vierkant, orde 6
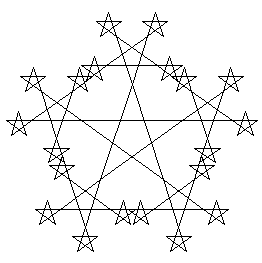
Pentagram, orde 2
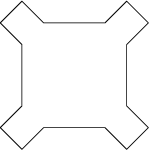
Sierpinsky ster, orde 0
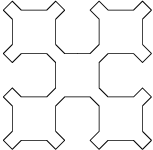
Sierpinsky ster, orde 1
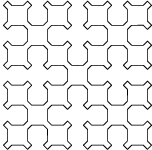
Sierpinsky ster, orde 2
© 2013-2025 webmasterij.nl | Disclaimer
| Contact | Privacy
Laatst bijgewerkt: 16 juni 2022