Vlakvullingen

Vlakvullingen zijn Iterated Function Systems (IFS), die niet tot de dendrieten gerekend worden. Er is echter geen fundamenteel verschil tussen dendrieten en vlakvullingen. Bij beide is er sprake van een Basis, een Axioma en een Motief, die oneindig worden herhaald. Ook zelfgelijkvormigheid is een belangrijke eigenschap. Het verschil zit uitsluitend in de figuur die ontstaat als je het verloop van de functie gaat tekenen.

Anders dan bij de dendrieten geeft dit type fractal in de limiet een volledige vulling van een deel van het platte vlak.

H-fractal

Probeer eens het volgende voorschrift (Basis en Axioma zijn gelijk; factor = 0,5):

Dit leidt in de limiet tot een volledige vlakvulling, die bekend staat als de H-Fractal:

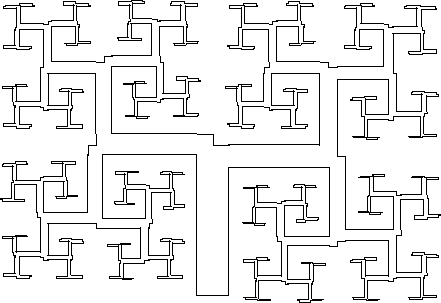
De van oorspong Poolse wiskundige Benoit Mandelbrot (1924-2010) heeft hier een variant op bedacht, die bekend staat als de Boom van Mandelbrot. Basis en motief worden getoond in het figuurtje hiernaast; de hele boom (getekend tot orde 7) staat hieronder. Merk op dat het motief per stap steeds wordt gespiegeld in de verticale as.

De Kromme van Lévy

Probeer eens het volgende voorschrift:

Als je dit herhaalt ontstaat de Kromme van Lévy.

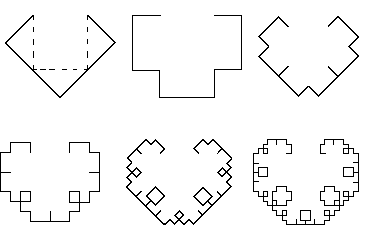
Hier is eenvoudig een vlakvulling van te maken, bijvoorbeeld door te beginnen met een vierkant:

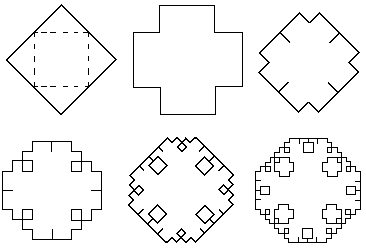
Deze fractal heet Tapijt van Lévy en is zeer
geschikt om te borduren!

Borduurpatroontjes?

Sommige fractals zijn zeer geschikt als borduurpatroon. Zoals bijvoorbeeld de Kruissteek-kromme, die in de limiet tweemaal de oppervlakte van het oorspronkelijke vierkant bedekt.
Basis en motief staan hiernaast. Het axioma wordt om-en-om toegepast, nl. eerst naar buiten, daarna naar binnen.

Een variant hierop krijg je als als je het motief verandert van een blokje in een punt. Het axioma wordt steeds in dezelfde richting toegepast.

Dit staat bekend als het Gescheurde vierkant of de Fractal van Cesàro.

Vlakvullende kronkellijnen

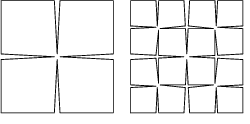
Niet alleen Iterated Function Systems kunnen zich als vlakvulling gedragen. Ook de zg. L-systems kunnen in de limiet een deel van het platte vlak vullen. Hieronder twee voorbeelden: de Krommen van Peano en Peano-Gosper.

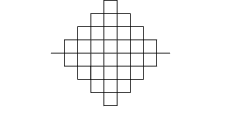
Peano kromme

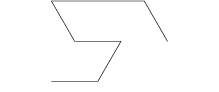
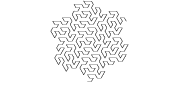
Peano-Gosper kromme

Tegelpatronen

De buitenste countour van de Peano-Gosper kromme wordt Gosper-eiland genoemd. Deze eilanden hebben de eigenschap perfect in elkaar te passen. Het tegelpatroon wat je hiermee kunt maken vult het gehele platte vlak.

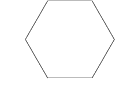
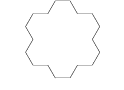
Ontwikkeling van een Gosper-eiland

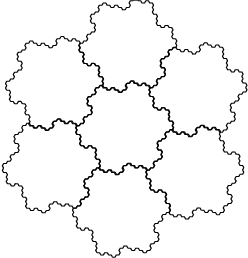
Tegelpatroon, opgebouwd uit Gosper-eilanden

De Kromme van Sierpinski

Ook Sierpinsky heeft zich bezig gehouden met vlakvullende figuren. Hieronder staat er een die bekend is als de Kromme van Sierpinski. Dit lijkt een sterfractal, maar is het niet!

Ruimtelijk

In het vorige hoofdstuk zijn de Zeef en het Tapijt van Sierpinski al genoemd. De vlakvulling ontstaat door het herhaald wegnemen van een deel van de basis-figuur.

De aanpak beperkt zich niet tot het vullen van het platte vlak. Ook de ruimte kan op deze wijze gedeeltelijk worden gvuld. Daar wordt hier niet verder op in gegaan. We beperken ons tot een voorbeeld, gebaseerd op het Tapijt van Sierpinski.

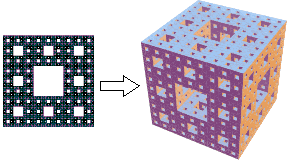
Deze figuur heet "Spons van Menger".

Laatst bijgewerkt: 4 december 2013