Kronkellijnen
De Engelse meteoroloog L.F. Richardson (1881-1913) heeft eens geprobeerd om de lengte te meten van de Westkust van Engeland. Ook probeerde hij de lengte van de grens tussen Spanje en Portugal te meten. Hij deed dat met behulp van landkaarten. Hij ontdekte dat, hoe gedetailleerder de kaart was, hoe langer de kustlijn en hoe langer de grens werd.
Dat lijkt vreemd, maar is het niet. Bij een kaart met grote schaalverhouding verdwijnen veel details (lees: "kronkels"); bij een grote schaalverhouding mist de meetlat veel details.
Je kunt natuurlijk ook de lengte van een kustlijn in het "echt" opmeten. Stel je voor dat je daarvoor een
meetlat van 100 meter lang gebruikt. Je zult dan veel minder "kronkels" mee kunnen nemen dan als je meetlat
'maar' 10 meter lang zou zijn.
Maar met een meetlat van 1 meter neem je weer méér kronkels mee dan met de meetlat van 10 meter mogelijk zou zijn.
De moraal van dit verhaal: Hoe korter de meetlat, hoe langer de kustlijn.
Het bijzondere van elke regelmatige of onregelmatige kronkellijn is dat elk stukje, hoe kort ook, een oneindige lengte heeft.
Als je de meetlengte steeds korter maakt, krijg je in de limiet een puntverzameling, net zoals bij de
Puntverzameling van Cantor. Het gevolg daarvan is dat elke kronkellijn in geen enkel
punt een raaklijn heeft!
Opmerking: In het bovenstaande is aangegeven dat elke kustlijn en elke landsgrens oneindig lang is. De lengte
die je meet hangt alleen af je de lengte van je meetlat!
Het ligt nu voor de hand om te denken dat dit alleen geldt voor willekeurige kronkellijnen. Maar dat is niet juist. Figuren
zoals een driehoek en een rechthoek hebben inderdaad een eindige omtrek, namelijk de som van lengten van de afzonderlijke
zijden. Maar realiseer je dat ook hier de lengte van de meetlat bepalend is. Als je een vierkant hebt met zijden van
10 cm lang en je meet die op met een meetlat met een lengte van 1 cm, zul je vinden dat de omtrek 40 cm is. Maar als
je een meetlat van 100 m lang gebruikt zul je vinden dat de omtrek "ongeveer nul" is...
Ook bij cirkels treedt wat vreemds op. De omtrek van een cirkel is gelijk aan πD, waarin D de diameter voorstelt.
Het getal π (pi) is ongeveer gelijk aan 3,141592654. Het aantal decimalen van π is echter oneindig groot. Hoe
meer decimalen van π je gebruikt, hoe groter de omtrek van de cirkel wordt!
Het verschil zit er in dat de omtrek van "normale" meetkundige figuren een eindige waarde heeft. De lengte van een kronkellijn is onbepaald.
Toen het fenomeen van de kronkellijnen werd ontdekt, aan het begin van de twintigste eeuw, werden deze lijnen aangeduid met de term "Pathologische Kromme". Inmiddels zijn we meer dan een eeuw verder en weten we dat kronkellijnen mede de basis vormen van wat wij aanduiden met "Fractal". Merk op dat ook hier sprake is oneindige herhaling. Net als in het voorgaande wordt de orde beperkt gehouden, zodat de figuren een beetje toonbaar blijven.
De Kromme van Von Koch
In 1904 beschreef de wiskundige H. Von Koch (1870-1924) een pathologische kromme die is opgebouwd volgens het volgende voorschrift:
- Verdeel een lijnstuk en drie gelijke stukken.
- Vervang het middelste stuk door twee gelijke stukken onder een hoek van 60°.




Onderstaande animatie toont de ontwikkeling van de Kromme van Von Koch, tot de orde 7.

Een variant op de Kromme van Koch is de Worst van Minkowski, die wordt gemaakt op basis van het volgende voorschrift: op een recht lijnstuk wordt een "blokgolf" gezet; Als de lengte van de basis gelijk is aan 1, liggen de drie tussenpunten op ¼, ½, resp. ¾.
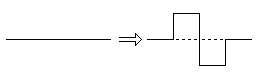
Als je dit axioma toepast tot de orde drie onstaat deze figuur:
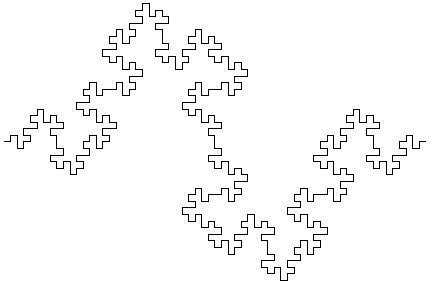
De Kromme van Lévy
Ook verwant aan de Kromme van Von Koch is de Kromme van Lévy. Deze is genoemd naar de Franse wiskundige P. Lévy (1886-1971).
Opmerking: De soort wiskundige bewerkingen waar deze figuren uit voortkomen worden meestal aangeduid met de term L-System, dat staat voor Lindenmayer System. Dit is genoemd naar de bedenker van een methode om de moeilijk te omschrijven axioma's toch betrekkelijk eenvoudig te formuleren.
De Drakenlijn
Deze kronkellijn is zo genoemd door J.E. Heighway, omdat het resultaat hem deed denken aan een Chinese draak.
Dit is een schoolvoorbeeld van een moeilijk te omschrijven axioma:
- Neem een lijnstuk (basis)
- **Gebruik een teller om het aantal stappen bij te houden, bijvoorbeeld n.
- Ga naar links als n = 1, 5, 9, 13, ...
- Ga naar rechts als n = 3, 7, 11, 15, ...
- Als n is even: Neem de richting van n/2. Bijvoorbeeld:
- als n = 10 gebruik je de richting van n = 5 (linksaf)
- als n = 12 gebruik je de richting van n = 6. Maar dat is even dus gebruik je de richting van n = 3 (rechtsaf).
Opmerkelijk is dat deze lijn zichzelf nergens snijdt. Binnen de "omtrek" van de lijn wordt het vlak regelmatig gevuld.
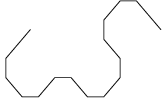
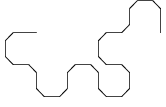
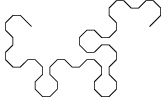
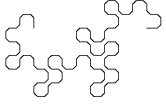
De onderstaande figuur toont de ontwikkeling van een variant van de drakenlijn, waarbij de hoekpunten
zijn "afgeschuind".
Merk op dat de afzonderlijke stappen steeds 45° verdraaid zijn getekend en dat de schaal van de tekening steeds kleiner wordt,
zodat de omvang van de figuur een beetje binnen de perken blijft.
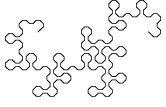
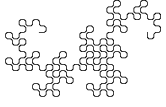
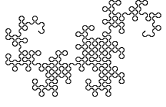
Andere vlakvullende kronkellijnen
In het voorgaande zijn de krommen van Peano en Peano-Gosper genoemd.
Een andere kronkellijn die hier niet mag ontbreken is de Hilbert-kromme, genoemd naar David Hilbert (1862-1943). Hieronder staat de ontwikkeling van één van vele vele verschijningsvormen van de Hilbert-kromme.





Eilanden
In de voorbeelden hierboven wordt steeds uitgegaan van een lijnstuk waarop een axioma wordt losgelaten. Dit is één van de kenmerken van de L-systems, maar het berperkt zich niet tot lijnstukken. Je kunt ook uitgaan van meetkundige figuren zoals een vierkant of een driehoek. Het axioma wordt dan uitgevoerd op elke zijde apart. Zie onderstaande figuren, waarvan de algemene naam "Eiland" is, of "Sneeuwvlok".
Von Koch Eiland: Sneeuwvlok
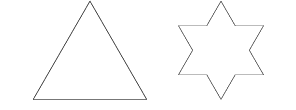
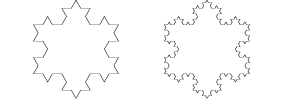
Er is uitgegaan van een gelijkzijdige driehoek. De kromme van Von Koch wordt op de drie zijden gemaakt, zodanig dat
de kromme aan de buitenzijde van de driehoek komt te liggen. Als je goed naar deze figuur kijkt zie je dat de oorspronkelijke
driehoek zelf niet meer terug te vinden is. Er zijn zes mogelijkheden voor de driehoek waarop dit eiland is gebaseerd...
Dit eiland staat ook bekend als de Sneeuwvlok van Von Koch.
Von Koch Eiland: Anti-sneeuwvlok
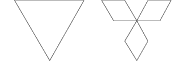
Er is uitgegaan van een gelijkzijdige driehoek. De kromme van Von Koch wordt op de drie zijden gemaakt, zodanig dat
de kromme aan de binnenzijde van de driehoek komt te liggen. De contouren van het eiland lijken verdacht veel op de
contour van het binnengebied in de Mandelbrot-set (waarover later meer).
Dit eiland staat ook bekend als de Anti-Sneeuwvlok van Von Koch.
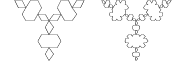
Minkowski Eiland

Hier boven een eiland dat is gemaakt van de Worst van Minkowski, uitgaande van een vierkant.
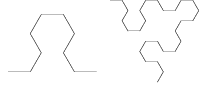
Pijlpunt van Sierpinsky
Sierpinski heeft zich heel veel beziggehouden met fractals. In het voorgaande is de Zeef van Sierpinski genoemd. Die is reeds getoond als boomstructuur en als vlakvulling.

Hieronder staat een versie die als kronkellijn is opgezet (getekend tot orde 4): De Pijlpunt van Sierpinski.

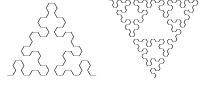
© 2013-2025 webmasterij.nl | Disclaimer
| Contact | Privacy
Laatst bijgewerkt: 4 december 2013