De Wiskunde achter Fractals

Fractals zijn meetkundige figuren. Om het gedrag van fractals te begrijpen, moet je dus iets van meetkunde (en ook andere takken van de wiskunde) af weten. Toch vind je hier geen uitgebreide wiskundige verhandelingen. Websites lenen zich daar niet voor. Een eenvoudige, goed te begrijpen inleiding (in het Nederlands!) staat op de site van Jan Stuivenberg. Echt diepgaande beschrijvingen zijn te vinden in de vele (helaas meestal Engelstalige) boeken over dit onderwerp. De echte internet-ridders (zij die geen boeken lezen ) kunnen ook eens gaan kijken op de site van Paul Bourke.

Hier beperken wij ons tot het beschrijven van de algoritmes waarmee de figuren worden gemaakt. Formules worden alleen gegeven als het echt niet anders kan.

Veel van de informatie en de hier beschreven fractals zijn ontleend aan het boek:

Hans Lauwerier
Fractals. Meetkundige Figuren in eindeloze herhaling
Uitg. Aramith, Bloemendaal
5e druk 1992
ISBN 90 6834 115 4

Dit boek is voor zover mij bekend niet meer verkrijgbaar.
Verder is ook dankbaar gebruik gemaakt van de informatie en van de illustraties op de site mathworld.wolfram.com.

Om een beetje inzicht te krijgen in het gedrag van fractals wordt eerst een onderverdeling gemaakt naar de "soort" figuur. We onderscheiden o.a.:

• Stoffractals (Puntverzamelingen)
• Dendrieten (Boomstructuren)
• Vlakvullingen
• Kronkellijnen
• Spiralen

Er wordt apart aandacht besteed aan de "Dimensie" van een Fractal en aan het fenomeen "Vreemde Aantrekker", die het gevolg zijn van het "chaotisch gedrag" van bepaalde wiskundige functies.

Tenslotte wordt een aantal meer ingewikkelde zaken beschreven, waaronder de Julia-set en de figuur waardoor fractals beroemd zijn geworden: De fractal van Mandelbrot. Daarbij wordt ook een paar daarvan afgeleide figuren beschreven, te weten Burning Ship en Buffalo.

Oneindige Herhaling is wat een fractal tot fractal maakt. De patronen die zich herhalen worden per stap steeds kleiner en vaak verandert de stand ten opzichte van het origineel. Deze eigenschap heet Gelijkvormigheid; het is tevens een kenmerkende eigenschap van fractals.
Het plaatje hieronder toont een zg. binaire boom. Dit is een fractal, zoals uit het volgende zal blijken.

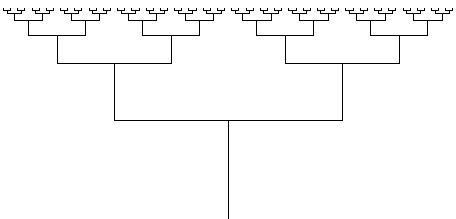
Deze boom wordt opgebouwd volgens een vast patroon:

1. Er wordt begonnen met een verticale stam.
2. Uit de stam komen twee horizontale takken; aan het uiteinde van elke tak ontstaat een nieuwe stam met lengte die de helft is van de "vorige".
3. Uit elke nieuwe stam komen weer twee horizontale takken.
4. Enzovoort.

De oorspronkelijke stam (1) wordt de Basis genoemd.
Het voorschrift (2) waaruit de takken en de nieuwe stammen omstaan heet Axioma.
Het resultaat heet Model of Motief. Het bevat tenminste één nieuwe basis, afhankelijk van het Axioma:

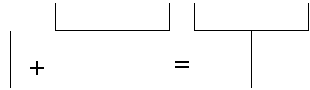
Basis + Axioma = Motief

Het motief bevat twee nieuwe bases.

Het aantal malen dat het axioma wordt uitgevoerd (of: het aantal niveaus waarin het motief in de figuur voorkomt) wordt aangeduid met Orde. De figuur hierboven is van orde 6. Het heeft weinig zin om een figuur van hogere orde te tekenen. De figuur loopt anders aan de bovenzijde dicht.

Bij deze boomfiguur vallen een paar dingen op:

• De figuur zelf zou een deel van een groter geheel kunnen zijn. Maar ook een deel van de figuur is een complete binaire boom. Er is dus sprake van gelijkvormigheid.
• De herhalingen gaan tot in het oneindige door.
• De verticale stammen worden steeds korter. De eerste stam heeft lengte 1, de tweede ½, de derde ¼, de vierde ⅛, enz. De takjes komen steeds dichter bij de bovenrand, maar blijven daar steeds een lengte van een een takje vandaan.
  Als je de lengte van de (verticale) takjes bij elkaar zou optellen en dat oneindig herhaalt krijg je:

  1 + ½ + ¼ + ⅛ + .... = 2

  De eindwaarde wordt nooit bereikt. De herhalingen gaan oneindig door en dus is deze binaire boom een fractal.
• De factor ½ die bij deze boom is gebruikt is overigens vrij willekeurig. Je zou net zo goed 0,333 of 0,576 kunnen nemen, zolang de factor maar tussen 0 en 1 ligt. De limiet waarde verandert daardoor wel!

Dit type fractal wordt Dendriet genoemd, van het Griekse woord dendron, dat "boom" betekent.
Op dit type fractals wordt verderop in deze verhandeling verder ingegaan.

Laatst bijgewerkt: 21 november 2020