Julia Fractals I:

Reële waarden van de constante

In de vorige hoofdstukken van deze verhandeling is gekeken naar het iteratie-proces:

x_n+1 = x_n^² + c

waarbij voor x en c reële getallen zijn genomen. Daarbij is in het bijzonder gekeken naar de oplossingen voor c = 0,0, c = -0,5 en c = -1,0. Op deze bladzijde gaan we dat weer doen, maar nu nemen we een complex getal z = x +iy als startwaarde. Het iteratieproces luidt dus nu:

z_n+1 = z_n^² + c

De oplossingen voor verschillende waarden van c liggen in het complexe vlak, omdat z complex is.

Opmerking:
Een verhandeling over complexe getallen vind je HIER.

Om te beginnen nemen we een reëel getal voor de constante c. Verderop in dit betoog worden voor c ook complexe waarden gebruikt.

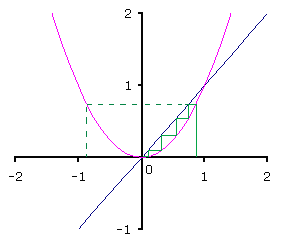c = 0
In het voorgaande hebben we gezien dat in het iteratieproces x_n+1 = x_n^² + 0 alle oplossingen van de startwaarden -1 ≤ x₀ ≤ +1 naar nul gaan. Zie de grafiek hier rechts.

Je zou ook kunnen zeggen: 'Alle startwaarden op een afstand (straal) van maximaal 1 gaan naar nul'.

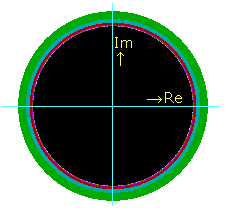Het ligt voor de hand om te veronderstellen dat dit in het complexe vlak ook gebeurt. Dat is inderdaad het geval, zie de figuur.
Alle punten binnen een cirkel met straal 1 zijn zwart gekleurd. Dat betekent dat ze worden aangetrokken.
Alle andere punten hebben een kleur. Dat betekent dat ze binnen een beperkt aantal stappen naar oneindig gaan.

Voor de volledigheid zijn de reële en de imaginaire as aangegeven.

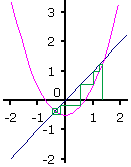c = -0,5
In het reële geval worden alle startwaarden -1,366 ≤ x₀ ≤ +1,366 naar -0,366 getrokken. De grenzen van dit interval liggen symmetrisch ten opzichte van de y-as, maar de aantrekker ligt niet meer op de symmetrie-as.

In het complexe geval zal er een symmetrische figuur ontstaan maar in elk geval geen cirkel. Zie de figuur hieronder.

 
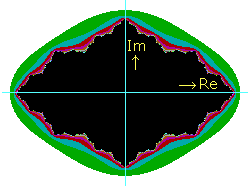
De rand van deze figuur is heel rafelig. Hij gedraagt zich als een fractal. Dat blijkt als je een stukje er van steeds verder uitvergroot. De patronen keren steeds weer terug.

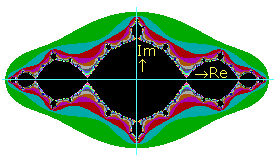c = -1
In het reële geval wordt voor c = -1 een dubbele aantrekker gevonden voor x = 0 en x = -1. Het aantrekgedrag zie je als het ware ontstaan doordat delen van de figuur voor c = -0,5 naar de reële of de imaginaire as worden getrokken. In het binnengebied van de (zwarte) figuur worden de assen nooit bereikt.
Zie de figuur hiernaast.

Complexe waarden van c
Reële waarden van c leveren figuren op die spiegel-symmetrisch zijn ten opzichte van de Reële en Imaginaire assen van het complexe vlak. Het volgende hoofdstuk van deze verhandeling onderzoekt wat er gebeurt als voor c complexe waarden genomen worden.

Laatst bijgewerkt: 8 december 2013