"Vreemde" Aantrekkers III:

Chaos

In het vorige hoofdstuk is genoemd dat er vreemde aantrekkers ontstaan in het iteratieproces voor het oplossen van: x_n+1 = x_n^² + c als c < -1,4.
Het gedrag van c bepaalt of er aantrekkers kunnen bestaan en of die "vreemd" kunnen zijn.

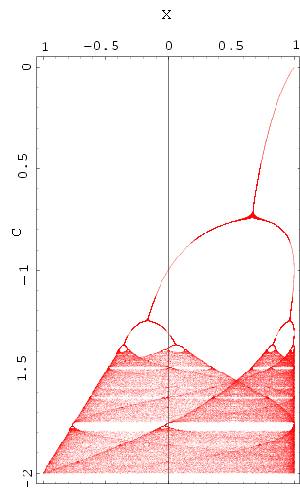In de figuur wordt dit geïllustreerd. De oplossing van x_n+1 = x_n^² + c is hier uitgezet tegen c.
Zoals je ziet is er één oplossing voor c > -0,75. Bij c = -0,75 treedt de eerste periodeverdubbeling op en als c nog wat kleiner wordt zijn er twee oplossingen voor de vergelijking.

Zonder verder in detail te treden wordt hier gemeld dat:

• Voor c > 0,25 is er geen aantrekker
  
• voor -0,75 < c < 0,25 is er een enkele aantrekker
  
• Voor -1,25 < c < -0,75 is er een dubbele aantrekker
  
• Voor -1,39 < c < -1,25 is er een vierdubbele aantrekker
  
• Voor -1,39 < c < -1,41 is er een achtdubbele aantrekker.
• Voor c < -2 zijn er geen aantrekkers meer.

Als c kleiner wordt dan ongeveer -1,41 (exact: c = -1,401155...) ontstaan de vreemde aantrekkers. Je ziet dat in de figuur: Er is geen sprake meer van duidelijke lijnen, maar een hele reeks willekeurige oplossingen, die "chaotisch" optreden. De voorspelbaarheid van de oplossing is verdwenen.
Merk op dat er in het "chaosgebied" weer gebieden zijn waar gewone aantrekkers zitten, bijvoorbeeld in de buurt van c = -1,76. Daar zit een drievoudige aantrekker. Uit elk van de drie oplossingen ontstaat door periodeverdubbeling weer een boomstructuur, die even later weer lijkt te verdwijnen in de chaos.

Er zijn echter veel meer van dit soort regelmatige gebiedjes in het chaosgebied. Uit deze figuur is dat niet gemakkelijk op te maken, vanwege de schaal waarop deze is getekend. Maar als je zou inzoomen op een dergelijk gebied zie je steeds weer nieuwe regelmatige gebiedjes optreden. Dit herhaalt zich oneindig, wat doet vermoeden dat dit een fractal is. Dat is inderdaad zo. Deze figuur is bekend als de Fractal van Feigenbaum, genoemd naar de Amerikaanse wiskundige Feigenbaum, die deze figuur in 1975 voor het eerst heeft beschreven.

De Fractal van Julia
Tot hier toe hebben we steeds gekeken naar het iteratieproces: x_n+1 = x_n^² + c, en hebben we voor x en c reële getallen genomen. Dat is echter niet strikt noodzakelijk. Je kunt het iteratieproces ook beginnen met complexe getallen, dus van de vorm z = x +iy. Ook voor de constante c kun je een complex getal gebruiken.

Ook bij dit soort functies treedt -afhankelijk van de waarde van c- chaotisch gedrag op. De rand van de gebieden in het complexe vlak waarbinnen aantrekking optreedt wordt aangeduid met Julia Set, naar de Franse wiskundige Gaston Maurice Julia (1893 - 1978), die in het begin van de twintigste eeuw voor het eerst onderzoek deed naar deze functies.
De (meestal prachtig gekleurde) grafische weergave van de gebieden rond de aantrekkers wordt Julia Fractal genoemd. Hier wordt in het volgende hoofdstuk verder op in gegaan.

Opmerking:
Een verhandeling over complexe getallen vind je HIER.

Laatst bijgewerkt: 5 december 2013