Julia Fractals III:
Complexe waarden van de constante
In het vorige hoofdstuk van deze verhandeling is gekeken naar het iteratie-proces:
zn+1 = zn² + c,
waarbij c een zuiver imaginair getal is. De oplossingen liggen allemaal in het complexe vlak, omdat z complex is.In het volgende gaan we kijken wat er gebeurt als het complexe getal c een reëel én een imaginair deel heeft, dus in c = x + iy zijn x ≠ 0 en y ≠ 0.
Opmerking:
Een verhandeling over complexe getallen vind je HIER.
In het voorgaande is geconstateerd dat:
- Zuiver reële waarden van c geven figuren die spiegel-symmetrisch zijn ten opzichte van de Reële en de Imaginaire as.
- Zuiver imaginaire waarden van c geven figuren die punt-symmetrisch zijn ten opzichte van de oorsprong. Verandering van het teken van c betekent een spiegeling in de Imaginaire as.
Deze twee effecten kun je combineren: c = x + iy. Het aantal mogelijkheden is legio. Hieronder staan er een paar. Steeds is aangegeven waar het middelpunt M van het plaatje zich bevindt in het complexe vlak, met daarbij de waarde van c. De getallen zijn afgerond op 4 decimalen om het een beetje leesbaar te houden.

M = 0,0044 - 0,0045i
c = -0,1082 + 0,9250i
Vergroting 1700 ×

M = 0,0079 - 0,0011i
c = -0,0990 + 0,8416i
Vergroting 233 ×
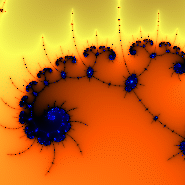
M = 1,3634 + 1,6178i
c = -1,2515 + 1,2442i
Vergroting 6,8 · 106 ×
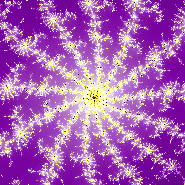
M = 0,2068 - 0,0374i
c = -0,2515 + 0,0606i
Vergroting 5,5 ×
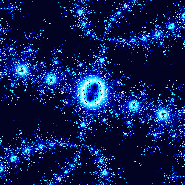
M = 0 + 0i
c = -1,0068 - 2,7868i
Vergroting 100 ×

M = 0 + 0i
c = -0,5020 + 0,5164i
Vergroting 2 ×
Merk op hoe belangrijk het kleurenpalet is om een mooi plaatje te krijgen. Hieronder zie je drie maal hetzelfde plaatje, maar ingekleurd met verschillende paletten.
M = 0 + 0i, c = -1,3959 + 0,0034i.

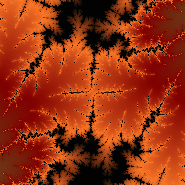

Je kunt je afvragen voor welke waarden van c er een Julia fractal zal gaan ontstaan en voor welke waarden
van c dat juist niet gebeurt.
Uit het voorgaande blijkt dat Julia fractals ontstaan als het iteratieproces
zn+1 = zn² + c
tenminste één aantrekker heeft. De vraag luidt dus:
Voor welke waarden van c zijn er aantrekkers,
en voor welke waarden van c zijn die er niet?
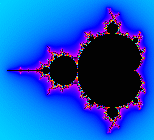 Het is mogelijk om de waarden van c waarvoor het iteratieproces aantrekkers heeft, te tekenen in het complexe vlak.
Er ontstaat dan een figuur die wel wat lijkt op een appel met een hoofd erop en die daarom het "Appelmannetje"
wordt genoemd. Dit is de beroemde Fractal van Mandelbrot, die is genoemd naar de Franse wiskundige
Benoit Mandelbrot (1924-2010), die hem rond 1975 voor het eerst beschreef.
Het is mogelijk om de waarden van c waarvoor het iteratieproces aantrekkers heeft, te tekenen in het complexe vlak.
Er ontstaat dan een figuur die wel wat lijkt op een appel met een hoofd erop en die daarom het "Appelmannetje"
wordt genoemd. Dit is de beroemde Fractal van Mandelbrot, die is genoemd naar de Franse wiskundige
Benoit Mandelbrot (1924-2010), die hem rond 1975 voor het eerst beschreef.
© 2013-2025 webmasterij.nl | Disclaimer
| Contact | Privacy
Laatst bijgewerkt: 21 november 2020